| Ligne 4 : | Ligne 4 : | ||
|Description=<translate>Mesurer la vitesse de rotation de la terre sur elle-même avec un gyromètre, comme ceux qui se trouvent dans les manettes de jeux, est un vrai petit défi. Ces gyromètres en effet, sont faits pour mesurer des vitesses de rotation imprimées aux manettes de jeux par des joueurs très réactifs… vitesses qui sont bien supérieures à la vitesse de rotation de notre vieille terre de 360° en 24H, soit 0.00417 °/s !</translate> | |Description=<translate>Mesurer la vitesse de rotation de la terre sur elle-même avec un gyromètre, comme ceux qui se trouvent dans les manettes de jeux, est un vrai petit défi. Ces gyromètres en effet, sont faits pour mesurer des vitesses de rotation imprimées aux manettes de jeux par des joueurs très réactifs… vitesses qui sont bien supérieures à la vitesse de rotation de notre vieille terre de 360° en 24H, soit 0.00417 °/s !</translate> | ||
|Area=Science and Biology | |Area=Science and Biology | ||
| − | |Type= | + | |Type=Technique |
|Difficulty=Hard | |Difficulty=Hard | ||
|Duration=7 | |Duration=7 | ||
| Ligne 18 : | Ligne 18 : | ||
| − | À la suite de cette intéressante lecture j’ai eu envie d’expérimenter à mon tour en partant d’un circuit élémentaire de mesure inertielle BNO055 et d’un banc de test de ma fabrication, afin de pouvoir tester plusieurs principes de mesure.</translate> | + | À la suite de cette intéressante lecture j’ai eu envie d’expérimenter à mon tour en partant d’un circuit élémentaire de mesure inertielle BNO055 et d’un banc de test de ma fabrication, afin de pouvoir tester plusieurs principes de mesure. |
| + | |||
| + | '''Vidéo d'introduction:''' | ||
| + | |||
| + | On y voit fonctionner le matériel qui a servi à enregistrer le signal très faible produit par la rotation terrestre sur le circuit de mesure inertielle posé sur un plateau tournant. | ||
| + | |||
| + | Le signal utile est prélevé à chaque fois que la rotation s'arrête pendant quelques secondes: A ce moment, la seule rotation "vue" par le circuit est la rotation terrestre (environ 4 millièmes de degrés par seconde). Ce n'est qu'après l'enregistrement de milliers d'échantillons que le signal utile sortira du bruit...</translate> | ||
}} | }} | ||
{{TutoVideo | {{TutoVideo | ||
| Ligne 24 : | Ligne 30 : | ||
|mp4video=VideoBanc .mp4 | |mp4video=VideoBanc .mp4 | ||
}} | }} | ||
| − | {{Materials}} | + | {{Materials |
| + | |Material=<translate></translate> | ||
| + | |Tools=<translate></translate> | ||
| + | }} | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=<translate>Le défi</translate> | |Step_Title=<translate>Le défi</translate> | ||
Version du 31 décembre 2023 à 09:43
Sommaire
- 1 Introduction
- 2 Video d'introduction
- 3 Étape 1 - Le défi
- 4 Étape 2 - Principes des mesures de rotation de la terre
- 5 Étape 3 - Le banc de mesure
- 6 Étape 4 - Configuration et acquisition des mesures avec le BNO055
- 7 Étape 5 - Mise au point des conditions de mesure (1/2)
- 8 Étape 6 - Mise au point des conditions de mesure (2/2)
- 9 Étape 7 - Résultats des mesures par différences entre deux positions (1/2)
- 10 Étape 8 - Résultats des mesures par différences entre deux positions (2/2)
- 11 Étape 9 - Résultats des mesures par modulation
- 12 Étape 10 - Conclusion et prolongements
- 13 Commentaires
Introduction
D’abord, rendons à Cesar ce qui est à Cesar ! L’idée de cette mesure vient d’un site internet qui publie des ressources pédagogiques dans le domaine de la science et de la technologie (www.pabr.org). La description de l’expérience initiale vaut le détour ! Cette expérience en effet part d’une manette de jeux posée sur un plateau de tourne-disques … (http://www.pabr.org/copernitron/copernitron.fr.html).
De plus l’article rappelle les différentes tentatives de mesures qui se sont déroulées principalement au XIXème siècle et dont le point d’orgue a été la célèbre expérience de Foucault avec son célèbre pendule ( https://fr.wikipedia.org/wiki/Pendule_de_Foucault ). On en retient que mettre en évidence directement la rotation de la terre par une mesure inertielle, n'est pas chose facile.
À la suite de cette intéressante lecture j’ai eu envie d’expérimenter à mon tour en partant d’un circuit élémentaire de mesure inertielle BNO055 et d’un banc de test de ma fabrication, afin de pouvoir tester plusieurs principes de mesure.
Vidéo d'introduction:
On y voit fonctionner le matériel qui a servi à enregistrer le signal très faible produit par la rotation terrestre sur le circuit de mesure inertielle posé sur un plateau tournant.
Le signal utile est prélevé à chaque fois que la rotation s'arrête pendant quelques secondes: A ce moment, la seule rotation "vue" par le circuit est la rotation terrestre (environ 4 millièmes de degrés par seconde). Ce n'est qu'après l'enregistrement de milliers d'échantillons que le signal utile sortira du bruit...Mp4
VideoBanc .mp4
Matériaux
Outils
Étape 1 - Le défi
La vitesse de rotation de la terre sur elle-même est de 360 / 24 / 3600 = 0.00417 °/s.
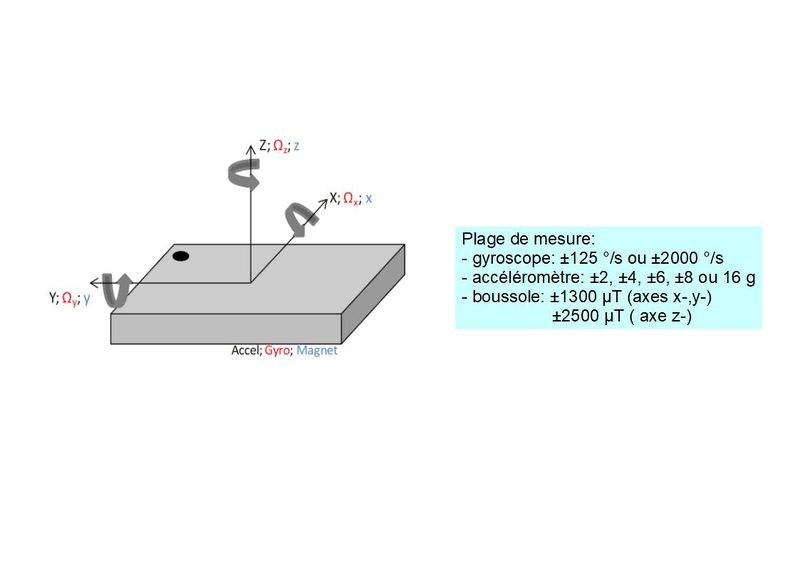
Pour faire cette mesure, on va utiliser le circuit intégré BNO055 de Bosch qui est un capteur inertiel réalisé en Technologie MEMS (Micro Electro-Mechanical System). Dans la partie gyromètre qui nous intéresse ici, une masse d’épreuve est mise en vibration et réagit aux rotations grâce à la force de Coriolis (https://www.youtube.com/watch?v=KiJ9xr8_GSI), comme le pendule de Foucault. En quelque sorte c’est un pendule de Foucault dans un circuit intégré…. Mais les dimensions ont été fantastiquement réduites, comme on peut le voir sur la figure 1....
Le défi réside dans l'utilisation de ce type de circuit à bas coût conçu pour les manettes de jeux. La plage de mesure la plus sensible est en effet de +/- 125 °/s, codée sur 16 bits (figure 2).
Dans ces conditions le pas de quantification est de 250 / 2^16 = 0.0038 °/s, très proche de la vitesse de rotation que l'on cherche à mesurer....
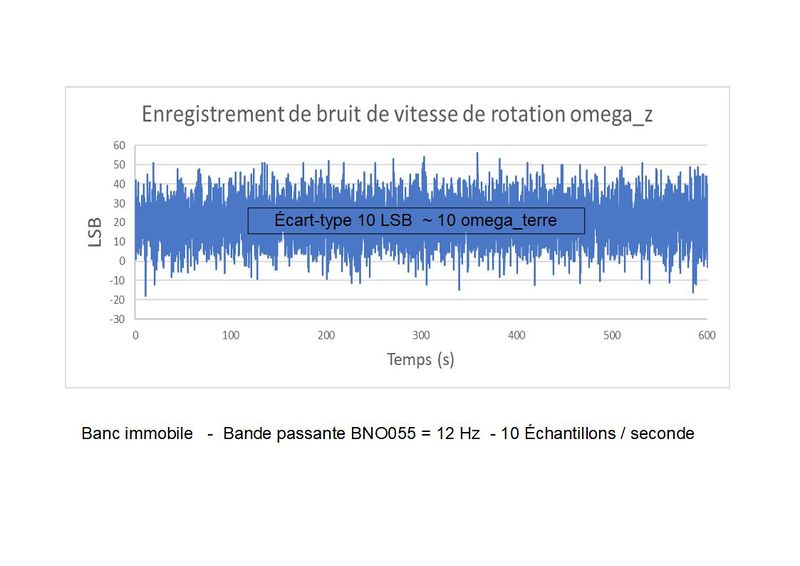
Heureusement il y a du bruit ! C'est ce qui va nous permettre de sortir du pas de quantification ...... sinon ce serait sans espoir de pouvoir faire une mesure de la rotation terrestre avec un minimum de précision !
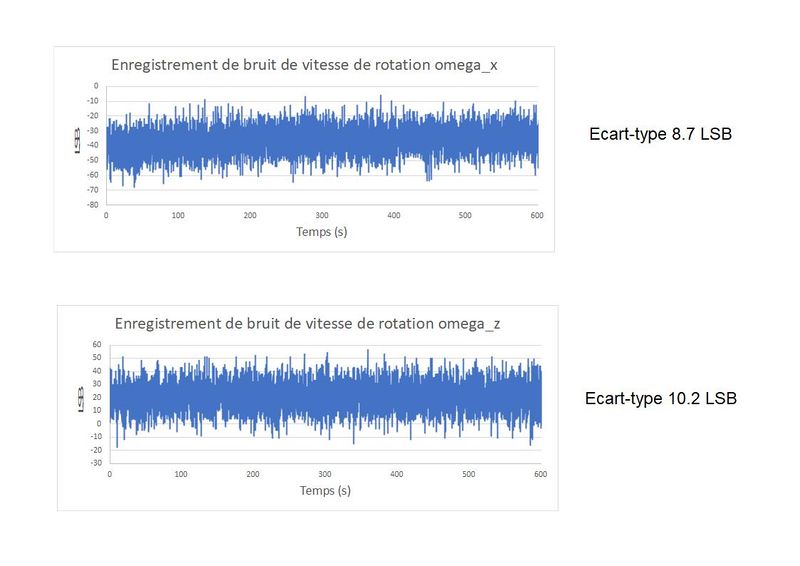
La figure 3 montre un enregistrement du bruit qui oscille sur près de 70 pas de quantification (LSB) en crête à crête, soit plus de 60 fois la valeur de la rotation terrestre ! On sent bien que la stratégie va être de moyenner de nombreuses mesures.... tout en évitant les dérives long terme et les biais...
Étape 2 - Principes des mesures de rotation de la terre
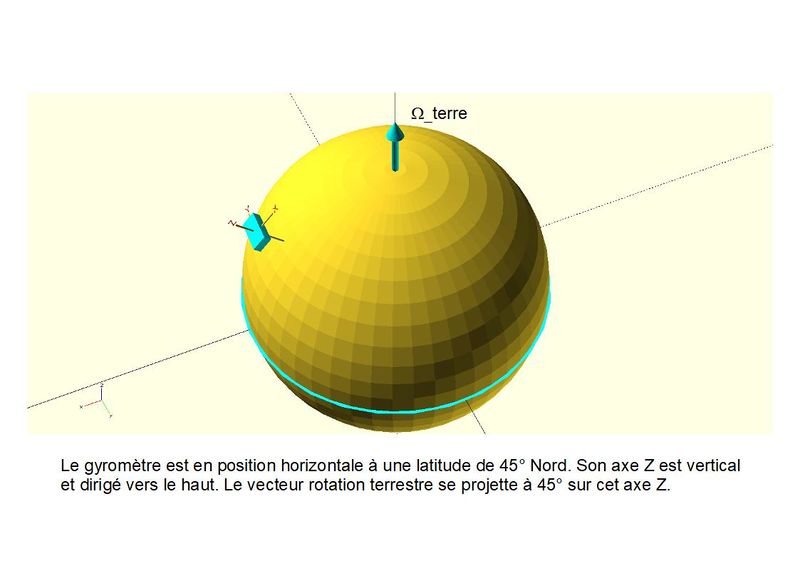
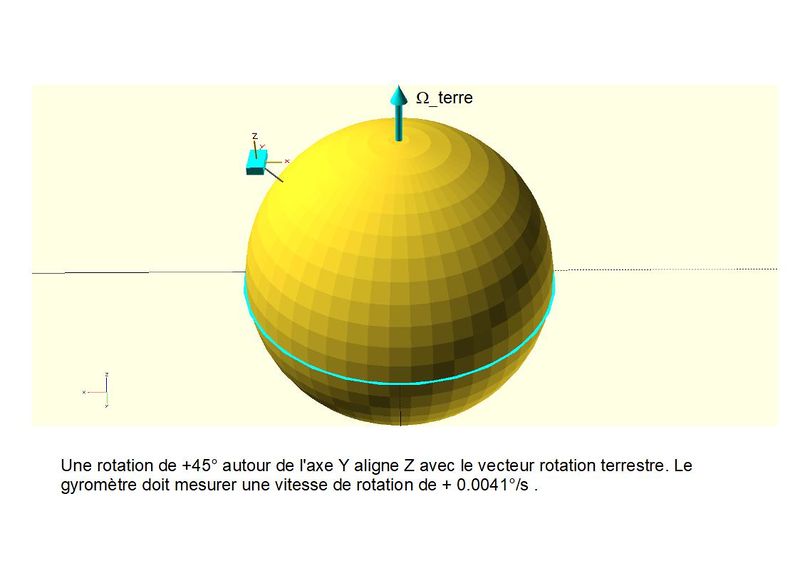
Le BNO055 en Occitanie....
Les 4 premières figures indiquent l'orientation du circuit lorsque l'expérience se déroule dans un coin d'Occitanie où la latitude est très proche de 45° Nord.
Mesures par différence entre deux positions
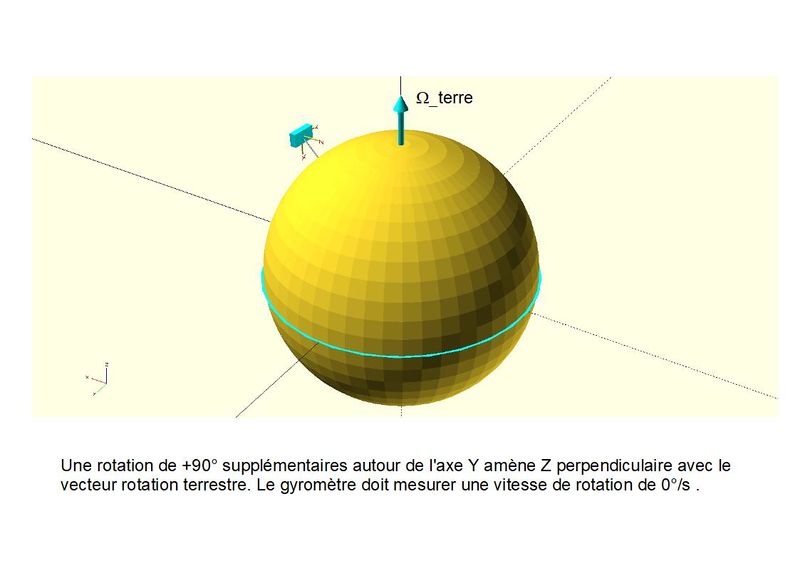
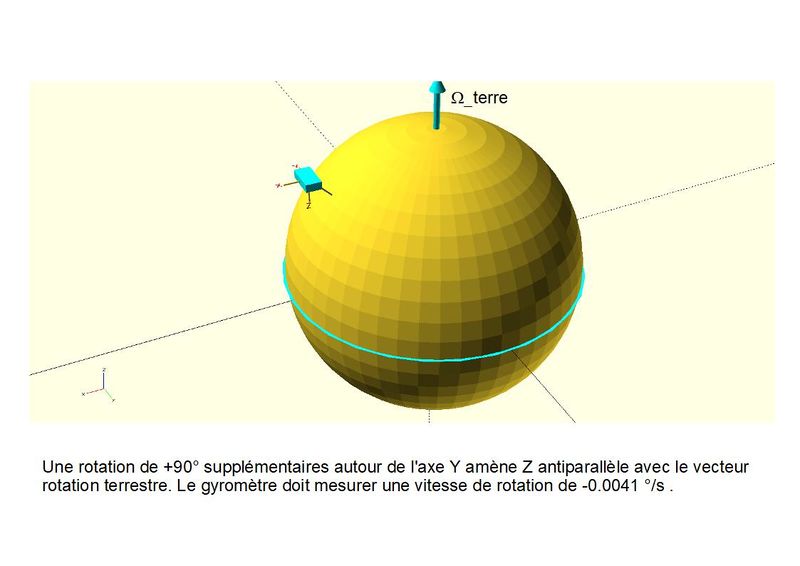
On ne peut pas mesurer directement des valeurs de la projection de Omega _terre car la réponse du capteur comporte toujours un offset inconnu. Par contre en faisant la différence entre deux mesures à deux positions différentes, on s'affranchit de cet offset. Par exemple la différence entre la position Z // Omega et Z antiparallèle à Omega nous donne deux fois la vitesse de rotation de la terre tout en annulant l'offset. De même la différence entre deux positions perpendiculaires à l'axe de rotation terre doit être égale à zéro.
Mesures par modulation sinusoïdale et analyse spectrale
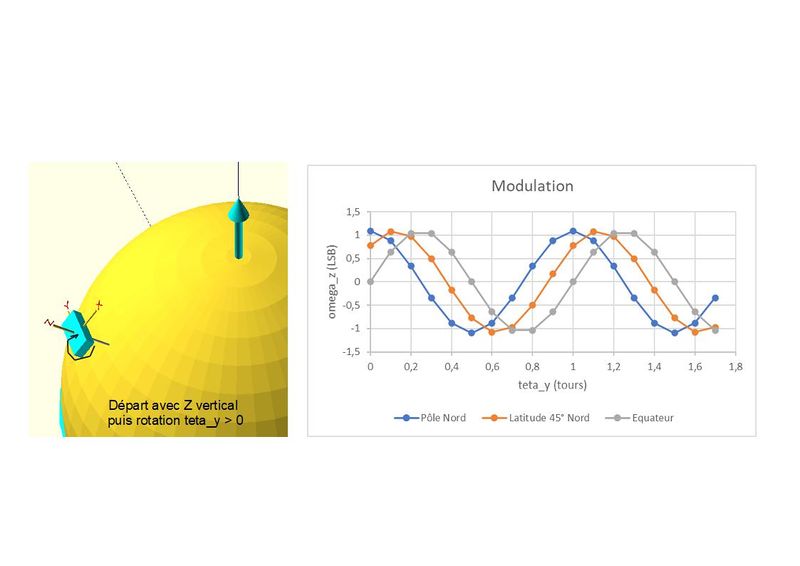
Si maintenant au lieu de se contenter de deux positions, on prélève une dizaine d'échantillons par tour, on va réaliser une modulation sinusoïdale de la valeur à mesurer. On obtiendra typiquement la sinusoïde de la figure 5.
Cette modulation ne sera pas visible car elle sera largement noyée dans le bruit. Heureusement la technique d'analyse spectrale par transformée de Fourier permettra de retrouver son amplitude (valeur de omega_terre) et même sa phase (position en latitude), comme nous le verrons plus bas.
Simulation des séquences d'acquisition
La dernière animation illustre la séquence de mesures par différence et par modulation sinusoïdale. Noter que chaque fois le changement entre deux positions stables se fait rapidement afin de ne pas perdre de temps.
Toutes les mesures se font en statique
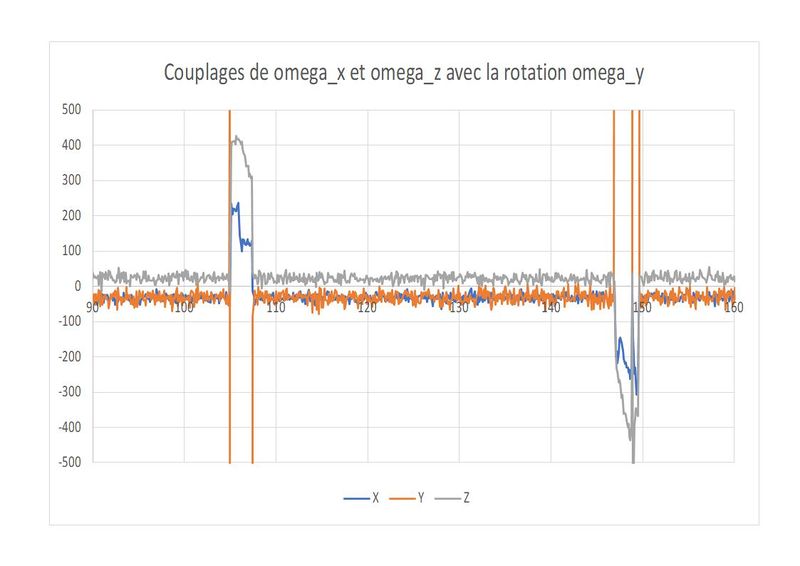
En effet toutes les acquisitions utiles se font uniquement sur les positions stables. La rotation du BNO055 autour de son axe Y avec une vitesse angulaire bien plus importante que celle de la terre "polluerait" notre mesure de façon importante à cause de couplages entre les axes. Par exemple celui généré par le non parallélisme entre l'axe Y et l'axe de rotation. En prenant les mesures pendant les périodes stables élimine totalement ce problème. La seule rotation qui existe alors est celle de la terre.
Étape 3 - Le banc de mesure
Constitution
Le banc de mesures est constitué par une planchette support qui tourne autour d’un axe horizontal, mu par un moteur pas à pas. Sur la planchette support se trouve une carte Arduino UNO avec un shield carte SD pour stocker les mesures de vitesse de rotation. A côté on a fixé le petit circuit supportant le gyromètre BNO055. Une pile pour l’alimentation et un interrupteur complètent le montage. Le moteur pas à pas est contrôlé par une autre carte Arduino UNO et un shield moteurs.
On peut trouver facilement tous ces composants, par exemple ici :
Shield SD : https://www.gotronic.fr/art-shield-carte-sd-v4-103030005-21518.htm
Moteur pas à pas : https://www.gotronic.fr/art-moteur-14hm11-0404s-23048.htm
Shield moteurs : https://www.gotronic.fr/art-commande-i2c-de-2-moteurs-cc-grove-108020103-29016.htm
Module Boussole BNO055 : https://www.gotronic.fr/art-module-boussole-bno055-27795.htm
Utilisation
Avec ce banc il est très facile de reproduire les séquences de mesure décrites au paragraphe précédent. Comme les rotations en effet se font autour de l'axe Y du BNO055, il suffit d'orienter le plan de rotation des vecteurs Z et X dans la direction Nord-Sud. Cette orientation étant faite, on déclenche l'enregistrement continu sur la carte des vitesses de rotation sur les 3 axes. Enfin on lance le programme de commande du moteur pas à pas pour balayer soit deux positions (mesure par différence de deux positions), soit pour échantillonner un certain nombre de positions par tour pendant plusieurs tours (analyse spectrale).
Étape 4 - Configuration et acquisition des mesures avec le BNO055
Tout d'abord le circuit BNO055 peut être exploité avec une interface I2C, après avoir fermé le pontet de sélection LK1 (http://www.robot-electronics.co.uk/files/BNO055-schematic.pdf).
De façon pratique, pour configurer et acquérir les mesures à partir d'une carte Arduino UNO, on a besoin d'un exemple type et de la notice du BNO055.
Cette notice peut être téléchargée ici:
https://www.bosch-sensortec.com/media/boschsensortec/downloads/datasheets/bst-bno055-ds000.pdf
D'autre part, le vendeur du circuit m'a fourni un exemple de programme pour acquérir les angles d'Euler, sans bibliothèque particulière, juste en s'aidant de la notice:
A l'aide de la notice Bosch et d'un minimum de concentration on peut configurer le circuit pour acquérir les vitesses de rotation autour des 3 axes, sur la plage de mesure la plus sensible +/- 125 °/s et avec la bande passante la plus réduite de 12 Hz:
Ce dernier fichier INO est documenté et renvoie aux pages utiles de la notice BOSCH pour les explications. Noter que ce programme permet d'enregistrer soit les angles d'Euler (clé = 0), soit les vitesses angulaires (clé = 1).
Je ne détaille pas plus mais je peux fournir des explications si besoin.
Étape 5 - Mise au point des conditions de mesure (1/2)
Choix de la sensibilité, de la bande passante et de la fréquence d'échantillonnage
Évidemment le choix du maximum de sensibilité s'impose afin de ne pas noyer le signal utile trop à l'intérieur du pas de quantification. Pour le gyromètre on choisira donc la plage +/- 125 °/s
Pour la bande passante, on choisit la plus basse, soit 12 Hz. En effet le signal de rotation terrestre ne varie pas très rapidement....
Ces deux paramètres sont décrits dans le tableau 3-9 de la notice (Gyroscope configurations).
La période d'échantillonnage est fixée à 0.1 seconde, de l'ordre de grandeur de la constante de temps du filtre (BP = 12 Hz). Une période plus petite ne permettrait pas de recueillir des échantillons indépendants car ils seraient corrélés avec ceux qui sont à l'intérieur d'une constante de temps du filtre. Une période d'échantillonnage plus grande ferait perdre des échantillons utiles pour le calcul de valeur moyenne de la mesure. En effet le rapport signal / bruit de la mesure s'améliore comme la racine carrée du nombre d'échantillons indépendants.
Choix de l'axe
D'après le principe de mesure, sur les 3 axes, seuls X et Z sont utilisables, Y étant réservé à la rotation. Pour faire ce choix, il y a plusieurs critères:
- le niveau de bruit: Pas très différent entre X et Z...(figure 1)
- la sensibilité au champ magnétique: Suite à un test avec un aimant, l'axe Z est le moins sensible. L'aimant utilisé produisant un champ magnétique beaucoup plus intense que le champ magnétique terrestre
- la sensibilité à la gravité: Ce point sera testé en utilisant deux configurations de mesure et sera discuté plus bas.
Mesure statique requise !
La figure 2 montre un enregistrement de vitesse de rotation sur les 3 axes, lorsque Y seul tourne, dans un sens puis dans l'autre. On y voit clairement que les mesures sur X et Z sont influencées par la rotation sur Y. Cette perturbation disparaît totalement lorsque la rotation autour de Y est arrêtée.
Étape 6 - Mise au point des conditions de mesure (2/2)
Optimisation de la durée d'intégration par échantillon
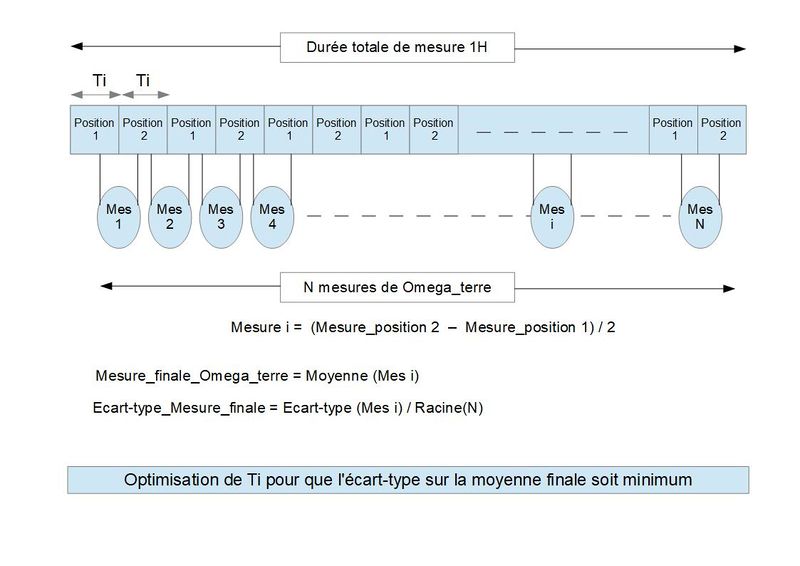
On va considérer une durée totale de mesure de 1Heure (figure 1).
Pendant cette heure on alterne entre deux positions stables (position 1 et position 2). A chaque position, on acquiert un certain nombre d’échantillons à la fréquence de 10 échantillons par seconde pendant un temps d’intégration Ti. Ces échantillons seront moyennés et constitueront un ensemble de mesures sur les positions stables.
La soustraction deux à deux de ces mesures (figure 1) donnera un ensemble de N valeurs de Omega_terre. En final, on fera la moyenne de ces N valeurs, sachant que l’écart type sur cette moyenne devrait s’améliorer comme la racine carrée de N. Ce sera notre valeur finale de Omega_terre pour 1H d’observation.
Cependant l’amélioration globale du signal à bruit en racine de N dépend de la caractéristique du bruit. Si le bruit comporte des variations lentes importantes plutôt que des variations plus rapides, le choix du temps d’intégration par échantillon Ti sera important. On imagine en effet que si Ti est important, la différence entre les deux positions sera largement influencée par ces dérives lentes.
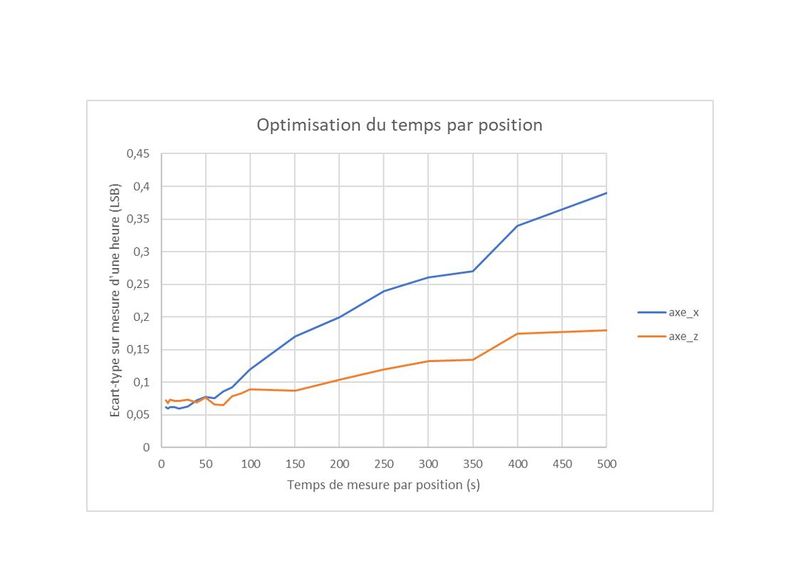
Aussi on a réalisé un enregistrement de 1 Heure de bruit, en l’absence de tout mouvement, et on a fait un découpage en temps Ti de valeurs différentes avant d’appliquer le traitement prévu pour les vrais échantillons.
Le résultat est donné sur le graphe de la figure 2, pour deux axes X et Z. Pour les deux axes, on constate que lorsque Ti dépasse 60 secondes on commence à voir une augmentation du bruit de mesure, ce qui traduit l’influence de dérives lentes. Ces dérives sont d’ailleurs plus importantes sur l’axe X que sur l’axe Z.
En résumé, pour nos mesures, on adoptera une Temps par position inférieur à 60 secondes.
Étape 7 - Résultats des mesures par différences entre deux positions (1/2)
Comme expliqué plus haut, vu le niveau très faible du signal recherché (environ 1 LSB) il se pourrait que certains biais soient bien plus importants que le signal recherché, en particulier l’effet de la gravité qui n’a pu être vérifié (voir Etape 5, Choix de l’axe).
Entre la position 1 et la position 2, la gravité n’agit pas de la même façon sur le BNO055.
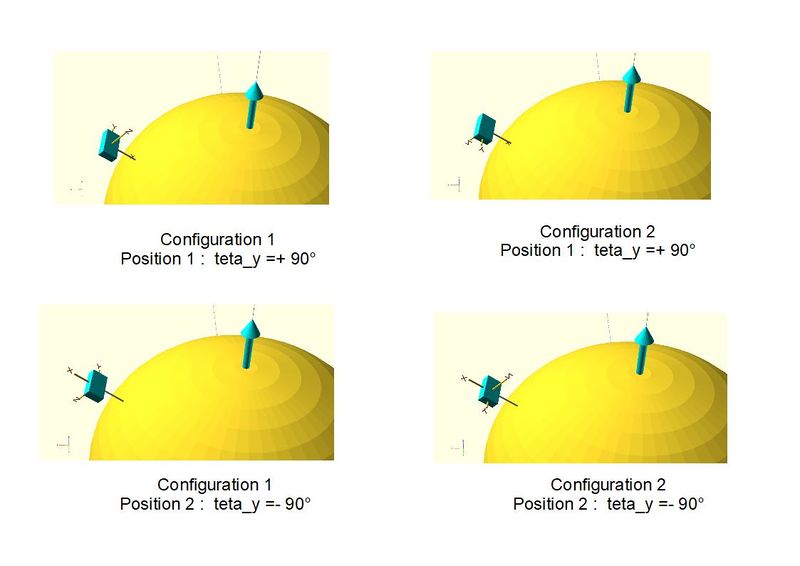
Afin d’estimer si la gravité a un effet sur la mesure de rotation de la terre, la procédure d’acquisition est la suivante (voir figure 1):
- Mesure entre deux positions, configuration 1
- Mesure entre les mêmes positions, configuration 2
Du point de vue de la gravité, les configurations 1 et 2 sont identiques. Du point de vue du signal à mesurer entre les deux positions, on doit avoir deux signaux de même valeur mais de signe opposé. On peut donc écrire:
[Pos 2 – Pos 1]Conf1 = G + 2 * Omega_terre * Cos(45°) (G = contribution gravité)
[Pos 2 – Pos 1]Conf2 = G - 2 * Omega_terre * Cos(45°) (G = contribution gravité)
Si la gravité n’a aucun effet, entre Conf 1 et Conf 2, on doit obtenir deux mesures de même amplitude mais de signe opposé.
Étape 8 - Résultats des mesures par différences entre deux positions (2/2)
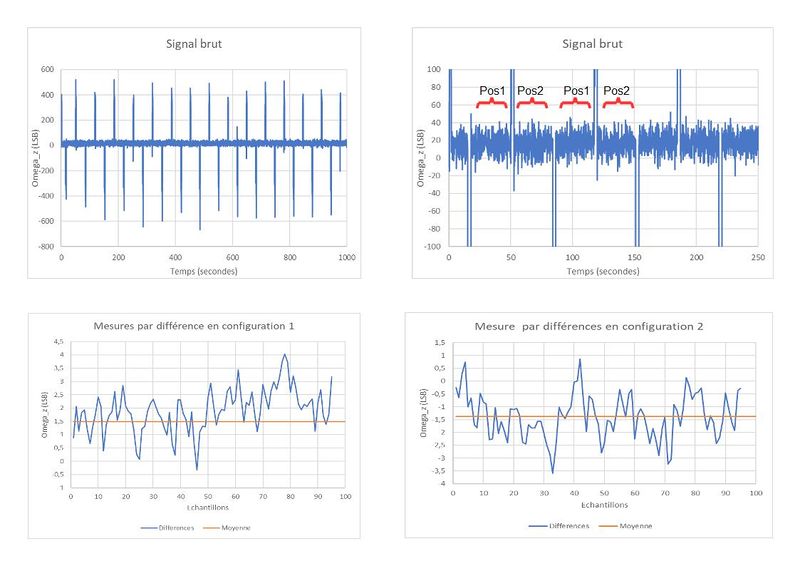
Haut , Gauche:
Enregistement sur 1000 secondes du signal Omega_z brut. On note des "spikes" de signal de plusieurs centaines de LSB. Ces spikes correspondent au couplage de Omega_z avec la rotation Omega_y qui permet de faire la navette entre une position stable et une autre. On ne retient bien sûr que les valeurs Omega_z enregistrées sur les positions après stabilisation.
Haut, Droite:
Omega_z est enregistré et moyenné pendant 30 secondes sur chacune des deux positions, ce qui donne des paires (Pos1, Pos2, Pos1, Pos2....).
Bas, Gauche:
On a tracé ici l'évolution des valeurs des différences entre paires en fonction de leur rang d'acquisition, pour la configuration 1. Ces différences devraient être identiques, au bruit près. La moyenne des 95 valeurs est de 1.48 LSB.
Bas, Droite:
On a tracé ici l'évolution des valeurs des différences entre paires en fonction de leur rang d'acquisition, pour la configuration 2. Ces différences devraient être identiques, au bruit près. La moyenne des 95 valeurs est de -1.38 LSB.
Conclusion 1: Les valeurs mesurées sont très proches en valeur absolue et bien de signe opposé. La gravité n'a donc pas d'influence majeure.
Conclusion 2: Les valeurs absolues trouvées sont très proches des prédictions de 1.54 LSB
Nota: Tous les traitements ont été réalisés avec EXCEL. Me laisser un commentaire auquel je répondrai si vous êtes intéressés par les détails.
Étape 9 - Résultats des mesures par modulation
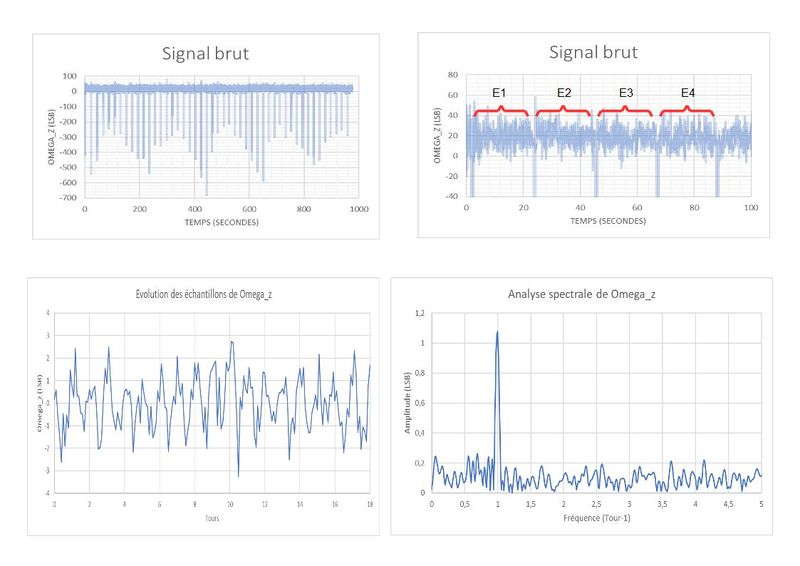
Haut , Gauche:
Enregistement sur 1000 secondes du signal Omega_z brut. On note des "spikes" de signal de plusieurs centaines de LSB. Ces spikes correspondent au couplage de Omega_z avec la rotation Omega_y qui permet de passer d'une position stable à une autre. On ne retient bien sûr que les valeurs Omega_z enregistrées sur les positions après stabilisation.
Haut, Droite:
Omega_z est enregistré et moyenné pendant 20 secondes sur chaque position stable, ce qui donne un échantillon de signal (E1, E2...) pour chacune des 10 positions stables pour chaque tour autour de Y (voir les principes à Étape 2).
Bas, Gauche:
On a tracé ici l'évolution des valeurs des échantillons en fonction des tours autour de l'axe Y. On devine une modulation de période 1 Tour noyée dans pas mal de bruit. On a ainsi enregistré au total 18 tours autour de Y, soit 18 * 20 * 10 = 3600 secondes de mesure effective.
Bas, Droite:
Le graphe donne le spectre de l'évolution précédente, obtenu par Transformée de Fourier. Ce spectre se réduit à un pic se détachant nettement sur un fond bruité. Ce pic correspond à notre signal rotation terrestre modulé à la fréquence de 1 période par Tour, soit à la fréquence de 1 Tour -1. La hauteur du pic représente la valeur de Oméga_terre. On trouve une valeur de presque 1.1 LSB, soit 0.0042 °/seconde pour une valeur recherchée de 0.00417 °/s. Mais il aura fallu 1H de mesure....
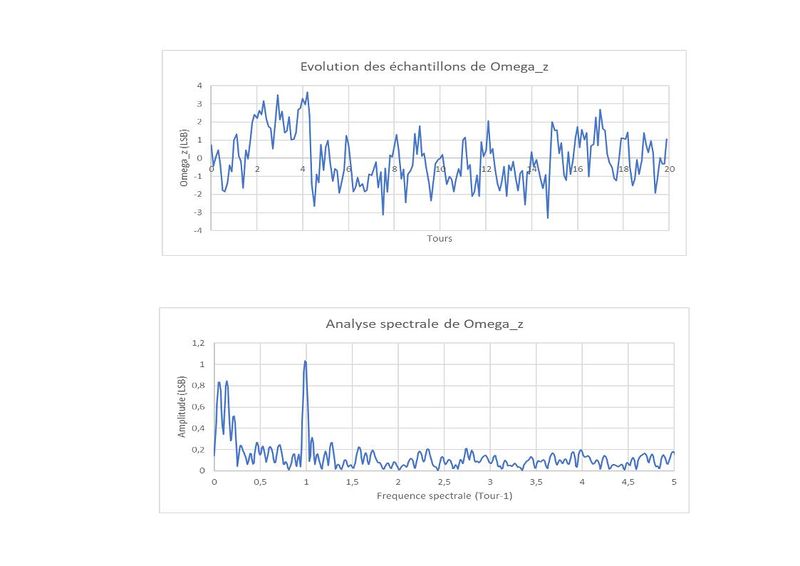
Sur la figure 2:
Une autre mesure est représentée où l'on peut voir des dérives lentes des échantillons, en plus du bruit habituel. Sur le spectre correspondant on voit apparaître ces perturbations à des fréquences inférieures à 0.5 Tour-1, ce qui ne perturbe pas la hauteur du pic utile à la fréquence de 1 Tour-1. C'est tout l'intérêt des méthodes de modulation et d'analyse spectrale pour séparer le signal utile de la majorité du bruit.
Nota: Tous les traitements ont été réalisés avec EXCEL. Me laisser un commentaire auquel je répondrai si vous êtes intéressés par les détails.
Étape 10 - Conclusion et prolongements
Quand j’ai commencé à me frotter à ce défi, je doutais sérieusement d’arriver à mesurer la vitesse de rotation de la terre avec une précision aussi bonne, même après 1 heure de mesure. C’est du niveau de ce que l’on pouvait obtenir avec un bon pendule de Foucault dans les années 1850… mais infiniment plus encombrant que ce petit circuit de quelques millimètres …. C’est une bonne surprise ! Et surtout j’ai pris beaucoup de plaisir à le faire !
J’espère que cela donnera l’envie à des lycéens et étudiants en sciences de reproduire ces mesures mais aussi d’aller plus loin. Ça pourrait être un beau sujet de traitement de signal que l'on peut traiter avec toute la rigueur mathématique (https://www.dunod.com/sciences-techniques/methodes-et-techniques-traitement-du-signal). Personnellement j'ai surtout cherché à donner envie.... Place aux jeunes !
Pour la suite on pourrait par exemple se donner l’objectif de repérer la direction du Nord géographique ainsi que sa position en latitude, tout cela en moins d’une heure. C’est typiquement le genre d’instrument dont aurait rêvé le capitaine Nemo dans son Nautilus tapi au fond des océans….
Bien sûr actuellement on dispose de gyromètres laser qui permettent de le faire beaucoup plus rapidement, mais totalement hors de portée d’un bricoleur…et extrêmement chers…
Bon courage et réussite à ceux qui voudront se lancer !
Published




 Français
Français English
English Deutsch
Deutsch Español
Español Italiano
Italiano Português
Português