Lampe en Carton façon voronoï : Différence entre versions

(set pageLanguageSource property)
(update property name)
 
(4 révisions intermédiaires par 2 utilisateurs non affichées)
Ligne 1 : Ligne 1 :
−
{{ {{tntn|Tuto Details}}
+
{{Tuto Details
 +
|Main_Picture=Lampe_en_Carton_façon_voronoï_20171218_175238.jpg
 +
|Licences=Attribution (CC BY)
 +
|Description=<translate><!--T:1--> Suspension pentagonale pour lampe  d'inspiration Voronoï.</translate>
 +
|Area=Decoration
 
|Type=Creation
 
|Type=Creation
−
|Area=Decoration
 
−
|Tags=lampe, decoupe laser, laser cutter, lamp, suspencion, pentagonale, pentagon
 
−
|Description=Voici comment réaliser une suspension pentagonale pour lampe en carton de récupération  d'inspiration Voronoï
 
 
|Difficulty=Easy
 
|Difficulty=Easy
 +
|Duration=1
 +
|Duration-type=hour(s)
 
|Cost=0
 
|Cost=0
 
|Currency=EUR (€)
 
|Currency=EUR (€)
−
|Duration=1
+
|Tags=suspencion, pentagonale, pentagon, Lampe, Découpe laser, Laser, Lumière, lampe
−
|Duration-type=hour(s)
 
−
|Licences=Attribution (CC BY)
 
−
|Main_Picture=Lampe_en_Carton_façon_voronoï_20171218_175238.jpg
 
 
|SourceLanguage=none
 
|SourceLanguage=none
 
|Language=fr
 
|Language=fr
 
|IsTranslation=0
 
|IsTranslation=0
 
}}
 
}}
−
{{ {{tntn|Introduction}}
+
{{Introduction
−
|Introduction=Réalisation n'est pas très compliqué. Cette suspension à pour idée de changer régulièrement de suspension dans mon appartement donc pas de gros frais en matières première...pour un rendu de qualité.
+
|Introduction=<translate><!--T:2--> La réalisation n'est pas très compliqué. L'idée est de changer régulièrement la suspension dans mon appartement, donc pas de gros frais en matières première, la lampe est  en carton de récupération. Mais le rendu est néanmoins de qualité !</translate>
 
}}
 
}}
−
{{ {{tntn|Materials}}
+
{{Materials
−
|Material=J'utilise des cartons de Pharmacie ou de parfumerie qui on un une texture plastifier, le carton qui fait offce de publicité et de tres bonne qualité et se découpe très bien a la découpeuse Laser.
+
|Material=<translate><!--T:3-->
−
|Tools=un cutter pour découper des morceaux de carton entrant dans la découpe laser, une agrafeuse ou de la colle, peinture en bombe si on veut changer de couleur
+
* Cartons de pharmacie ou de parfumerie qui on un une texture plastifiée
−
|Tuto_Attachments={{ {{tntn|Tuto Attachments}}
+
Le carton qui fait office de publicité et de très bonne qualité et se découpe très bien à la découpeuse Laser.</translate>
 +
|Tools=<translate><!--T:4-->
 +
* Cutter
 +
* Découpe laser
 +
* Agrafeuse ou de la colle
 +
* Peinture en bombe</translate>
 +
|Tuto_Attachments={{Tuto Attachments
 
|Attachment=Lampe voronoi.dxf
 
|Attachment=Lampe voronoi.dxf
−
}}{{ {{tntn|Tuto Attachments}}
+
}}{{Tuto Attachments
 
|Attachment=Lampe voronoi modification culot.dxf
 
|Attachment=Lampe voronoi modification culot.dxf
−
}}{{ {{tntn|Tuto Attachments}}
+
}}{{Tuto Attachments
 
|Attachment=Lampe voronoi.pdf
 
|Attachment=Lampe voronoi.pdf
−
}}{{ {{tntn|Tuto Attachments}}
+
}}{{Tuto Attachments
 
|Attachment=Lampe voronoi modification culot.pdf
 
|Attachment=Lampe voronoi modification culot.pdf
 
}}
 
}}
 
}}
 
}}
−
{{ {{tntn|Separator}}}}
+
{{Separator}}
−
{{ {{tntn|Tuto Step}}
+
{{Tuto Step
−
|Step_Title=Trouver du Carton
+
|Step_Title=<translate><!--T:5--> Trouver du carton</translate>
−
|Step_Content=l’étape principale est de trouver du carton, dans certaines villes, un jour est dédié au ramassage des carton alors c'est le bon moment pour faire le tour non loin des pharmacie ou parfumerie qui  se séparent de leur cartons publicitaires...
+
|Step_Content=<translate><!--T:6--> L’étape principale est de trouver du carton. Dans certaines villes, un jour est dédié au ramassage des carton, c'est alors le bon moment pour faire le tour des pharmacie ou parfumerie qui  se séparent de leur cartons publicitaires...</translate>
 +
|Step_Picture_00=Lampe_en_Carton_façon_voronoï_20171219_155916.jpg
 
}}
 
}}
−
{{ {{tntn|Tuto Step}}
+
{{Tuto Step
−
|Step_Title=Préparer la découpe
+
|Step_Title=<translate><!--T:7--> Préparer la découpe</translate>
−
|Step_Content=Découper le carton a la taille de votre lampe, Attention vu les pliage elle est souvent trop petite donc n’hésitez pas à voir grand...
+
|Step_Content=<translate><!--T:8-->
 +
Découper le carton à la taille de votre lampe, Attention vu les pliages elle est souvent trop petite donc n’hésitez pas à voir grand...
 +
 
 +
<!--T:9-->
 +
L'élément principal ici est la mesure et l’adaptation de la suspension au support de l'ampoule, dans l'exemple choisi j'ai utilisé un culot de 33 mm. La suspension rentre un peu en force mais comme ça pas de problème de décrochage.
  
−
L'élément principal ici est la mesure et l’adaptation de la suspension au support de l'ampoule, dans l'exemple choisi j'ai utilisé un culot de 33mm. La suspension rentre un peut en force mais comme ça pas de problème de décrochage.
+
<!--T:20-->
 +
Fichier : [[:Fichier:Lampe voronoi modification culot.pdf|Lampe Voronoi modification culot.pdf]]</translate>
 +
|Step_Picture_00=Lampe_en_Carton_façon_voronoï_Voronoi.png
 
}}
 
}}
−
{{ {{tntn|Tuto Step}}
+
{{Tuto Step
−
|Step_Title=Découper les fichier
+
|Step_Title=<translate><!--T:10--> Découper les fichiers</translate>
−
|Step_Content=Avec votre découpeuse laser découpe donc les carton, attention deux puissance sont necessaire :
+
|Step_Content=<translate><!--T:11-->
 +
Avec votre découpeuse laser découper les cartons. Attention deux puissance sont nécessaire :
 +
* le trait rouge (découpe) : vitesse 120mm/s à 60w
 +
* le trait Noir (pliage) : vitesse 120 mm/s à 25w</translate>
 +
|Step_Picture_00=Lampe_en_Carton_façon_voronoï_20171219_162728.jpg
 +
}}
 +
{{Tuto Step
 +
|Step_Title=<translate><!--T:12--> Monter la lampe</translate>
 +
|Step_Content=<translate><!--T:13-->
 +
Assemblage de la lampe, mise des languettes dans les encoches, je bloque tout avec une agrafe, ou vous pouvez utiliser de la colle, dans se cas des pinces à linge pour maintenir en contact.
  
−
le trait rouge (découpe) : vitesse 120mm/s à 60w
+
<!--T:21-->
 +
Peindre à la bombe.
  
−
le trait Noir (pliage) : vitesse 120 mm/s à 25w
+
<!--T:14-->
 +
Installation sur l'applique du plafonnier.</translate>
 +
|Step_Picture_00=Lampe_en_Carton_façon_voronoï_20171218_175148.jpg
 +
|Step_Picture_01=Lampe_en_Carton_façon_voronoï_20171218_175144.jpg
 
}}
 
}}
−
{{ {{tntn|Tuto Step}}
+
{{Tuto Step
−
|Step_Title=Monatge de la lampe
+
|Step_Title=<translate><!--T:15--> Résultat final</translate>
−
|Step_Content=Assemblage de la lampe, mise des languettes dans les encoches, je bloque tout avec une agrafe, ou vous pouvez utiliser de la colle, dans se cas des pince a linge pour maintenir en contact.  
+
|Step_Content=<translate><!--T:16--> Fiat lux !</translate>
 +
|Step_Picture_00=Lampe_en_Carton_façon_voronoï_20171218_175238.jpg
 +
}}
 +
{{Notes
 +
|Notes=<translate><!--T:17-->
 +
En mathématiques, un '''diagramme de Voronoï''' est un découpage du plan (pavage) en cellules à partir d'un ensemble discret de points appelés « germes ». Chaque cellule enferme un seul germe, et forme l'ensemble des points du plan plus proches de ce germe que de tous les autres. La cellule représente en quelque sorte la « zone d'influence » du germe.
  
−
Installation sur l'applique du plafonnier
+
<!--T:18-->
−
}}
+
Le diagramme doit son nom au mathématicien russe Gueorgui Voronoï (1868 - 1908), et est aussi appelé '''décomposition de Voronoï''', '''partition de Voronoï''', '''polygones de Voronoï''', '''tessellation de Dirichlet''' ou '''polygones de Thiessen'''.
−
{{ {{tntn|Notes}}
+
 
−
|Notes=
+
<!--T:19-->
 +
De manière plus générale, il représente une décomposition particulière d’un espace métrique déterminée par les distances à un ensemble discret d’objets de l’espace, en général un ensemble discret de points. ([https://fr.wikipedia.org/wiki/Diagramme_de_Vorono%C3%AF Wikipédia : Diagramme de Voronoï])</translate>
 
}}
 
}}
−
{{ {{tntn|Tuto Status}}
+
{{Tuto Status
−
|Complete=Draft
+
|Complete=Published
 
}}
 
}}

Version actuelle datée du 9 décembre 2019 à 11:40

Suspension pentagonale pour lampe d'inspiration Voronoï.

Auteur avatarSylvain Roux | Dernière modification 9/12/2019 par Clementflipo

Lampe en Carton façon voronoï 20171218 175238.jpg
Difficulté
Facile
Durée
1 heure(s)
Catégories
Décoration
Coût
0 EUR (€)
Suspension pentagonale pour lampe d'inspiration Voronoï.
Difficulté
Facile
Durée
1 heure(s)
Catégories
Décoration
Coût
0 EUR (€)
Autres langues :
français
Licence : Attribution (CC BY)

Introduction

La réalisation n'est pas très compliqué. L'idée est de changer régulièrement la suspension dans mon appartement, donc pas de gros frais en matières première, la lampe est en carton de récupération. Mais le rendu est néanmoins de qualité !

Matériaux

  • Cartons de pharmacie ou de parfumerie qui on un une texture plastifiée

Le carton qui fait office de publicité et de très bonne qualité et se découpe très bien à la découpeuse Laser.

Outils

  • Cutter
  • Découpe laser
  • Agrafeuse ou de la colle
  • Peinture en bombe

Lampe voronoi.dxf
Lampe voronoi modification culot.dxf
Lampe voronoi.pdf
Lampe voronoi modification culot.pdf

Étape 1 - Trouver du carton

L’étape principale est de trouver du carton. Dans certaines villes, un jour est dédié au ramassage des carton, c'est alors le bon moment pour faire le tour des pharmacie ou parfumerie qui se séparent de leur cartons publicitaires...

Lampe en Carton façon voronoï 20171219 155916.jpg




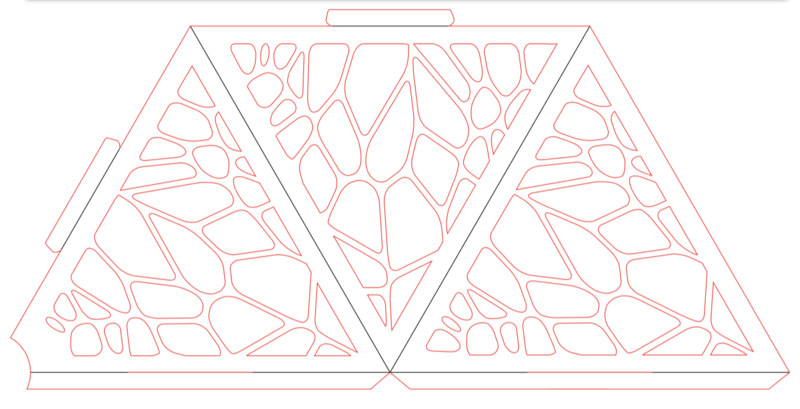
Étape 2 - Préparer la découpe

Découper le carton à la taille de votre lampe, Attention vu les pliages elle est souvent trop petite donc n’hésitez pas à voir grand...

L'élément principal ici est la mesure et l’adaptation de la suspension au support de l'ampoule, dans l'exemple choisi j'ai utilisé un culot de 33 mm. La suspension rentre un peu en force mais comme ça pas de problème de décrochage.

Fichier : Lampe Voronoi modification culot.pdf

Lampe en Carton façon voronoï Voronoi.png




Étape 3 - Découper les fichiers

Avec votre découpeuse laser découper les cartons. Attention deux puissance sont nécessaire :

  • le trait rouge (découpe) : vitesse 120mm/s à 60w
  • le trait Noir (pliage) : vitesse 120 mm/s à 25w
Lampe en Carton façon voronoï 20171219 162728.jpg




Étape 4 - Monter la lampe

Assemblage de la lampe, mise des languettes dans les encoches, je bloque tout avec une agrafe, ou vous pouvez utiliser de la colle, dans se cas des pinces à linge pour maintenir en contact.

Peindre à la bombe.

Installation sur l'applique du plafonnier.

Lampe en Carton façon voronoï 20171218 175148.jpg
Lampe en Carton façon voronoï 20171218 175144.jpg



Étape 5 - Résultat final

Fiat lux !

Lampe en Carton façon voronoï 20171218 175238.jpg




Notes et références

En mathématiques, un diagramme de Voronoï est un découpage du plan (pavage) en cellules à partir d'un ensemble discret de points appelés « germes ». Chaque cellule enferme un seul germe, et forme l'ensemble des points du plan plus proches de ce germe que de tous les autres. La cellule représente en quelque sorte la « zone d'influence » du germe.

Le diagramme doit son nom au mathématicien russe Gueorgui Voronoï (1868 - 1908), et est aussi appelé décomposition de Voronoï, partition de Voronoï, polygones de Voronoï, tessellation de Dirichlet ou polygones de Thiessen.

De manière plus générale, il représente une décomposition particulière d’un espace métrique déterminée par les distances à un ensemble discret d’objets de l’espace, en général un ensemble discret de points. (Wikipédia : Diagramme de Voronoï)

Commentaires

Published

Récupérée de « https://wikifab.org/w/index.php?title=Lampe_en_Carton_façon_voronoï&oldid=71929 »
© 2017 - 2024 Dokit, SAS.