| (2 révisions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 3 : | Ligne 3 : | ||
|Main_Picture_annotation={"version":"3.5.0","objects":[{"type":"image","version":"3.5.0","originX":"left","originY":"top","left":-1,"top":-43,"width":763,"height":804,"fill":"rgb(0,0,0)","stroke":null,"strokeWidth":0,"strokeDashArray":null,"strokeLineCap":"butt","strokeDashOffset":0,"strokeLineJoin":"miter","strokeMiterLimit":4,"scaleX":0.79,"scaleY":0.79,"angle":0,"flipX":false,"flipY":false,"opacity":1,"shadow":null,"visible":true,"clipTo":null,"backgroundColor":"","fillRule":"nonzero","paintFirst":"fill","globalCompositeOperation":"source-over","transformMatrix":null,"skewX":0,"skewY":0,"crossOrigin":"","cropX":0,"cropY":0,"src":"https://wikifab.org/images/b/b2/Triangul_Aire_IMG_6849.png","filters":[]}],"height":450.95541401273886,"width":600} | |Main_Picture_annotation={"version":"3.5.0","objects":[{"type":"image","version":"3.5.0","originX":"left","originY":"top","left":-1,"top":-43,"width":763,"height":804,"fill":"rgb(0,0,0)","stroke":null,"strokeWidth":0,"strokeDashArray":null,"strokeLineCap":"butt","strokeDashOffset":0,"strokeLineJoin":"miter","strokeMiterLimit":4,"scaleX":0.79,"scaleY":0.79,"angle":0,"flipX":false,"flipY":false,"opacity":1,"shadow":null,"visible":true,"clipTo":null,"backgroundColor":"","fillRule":"nonzero","paintFirst":"fill","globalCompositeOperation":"source-over","transformMatrix":null,"skewX":0,"skewY":0,"crossOrigin":"","cropX":0,"cropY":0,"src":"https://wikifab.org/images/b/b2/Triangul_Aire_IMG_6849.png","filters":[]}],"height":450.95541401273886,"width":600} | ||
|Licences=Attribution (CC BY) | |Licences=Attribution (CC BY) | ||
| − | |Description=<translate> | + | |Description=<translate>Conception : Séphane Cordier et Camille Bisson |
| − | + | Triangul'Aire est un ensemble d'objets pédagogiques qui permettent de comprendre la formule de l'aire d'un triangle. | |
| + | |||
| + | Ce premier objet permet de montrer que pour n'importe quel triangle ayant la même base et la même hauteur, l'aire (symbolisée par le nombre de billes) ne change pas, quel que soit la longueur des 2 autres côtés.</translate> | ||
|Area=Science and Biology | |Area=Science and Biology | ||
|Type=Creation | |Type=Creation | ||
| Ligne 45 : | Ligne 47 : | ||
}}{{Tuto Attachments | }}{{Tuto Attachments | ||
|Attachment=Triangul_Aire_manette-pmma-3mm.svg | |Attachment=Triangul_Aire_manette-pmma-3mm.svg | ||
| + | }}{{Tuto Attachments | ||
| + | |Attachment=Triangul_Aire_notice.pdf | ||
}} | }} | ||
}} | }} | ||
| Ligne 56 : | Ligne 60 : | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=<translate>Assemblage de la boîte</translate> | |Step_Title=<translate>Assemblage de la boîte</translate> | ||
| − | |Step_Content=<translate>1. Assembler les parois en | + | |Step_Content=<translate>1. Assembler les parois en PMMA sur la plaque intermédiaire en bois (cf figure 1) |
2. Assembler les cotés et le dessous (cf figure 2) | 2. Assembler les cotés et le dessous (cf figure 2) | ||
| Ligne 72 : | Ligne 76 : | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=<translate>Ajout des billes</translate> | |Step_Title=<translate>Ajout des billes</translate> | ||
| − | |Step_Content=<translate>#Coller les tiges en | + | |Step_Content=<translate>#Coller les tiges en PMMA (cf figure 5) |
| − | #Insérer les tiges en | + | #Insérer les tiges en PMMA, entre les parois en PMMA, les faire passer dans les trous de la plaque intermédiaire. |
| − | #Verser les | + | #Verser les billes entre les tiges (si besoin fabriquez-vous un entonnoir en papier) en les resserrant petit à petit. |
#Rejoindre les extrémités des tiges avec les manettes et une vis de 3mm (cf figure 7) | #Rejoindre les extrémités des tiges avec les manettes et une vis de 3mm (cf figure 7) | ||
#Refermer la boite</translate> | #Refermer la boite</translate> | ||
| Ligne 92 : | Ligne 96 : | ||
}} | }} | ||
{{Tuto Status | {{Tuto Status | ||
| − | |Complete= | + | |Complete=Published |
}} | }} | ||
Version actuelle datée du 15 avril 2024 à 14:53
Conception : Séphane Cordier et Camille Bisson
Triangul'Aire est un ensemble d'objets pédagogiques qui permettent de comprendre la formule de l'aire d'un triangle.
Ce premier objet permet de montrer que pour n'importe quel triangle ayant la même base et la même hauteur, l'aire (symbolisée par le nombre de billes) ne change pas, quel que soit la longueur des 2 autres côtés. Difficulté
Facile
Durée
2 heure(s)
Catégories
Science & Biologie
Coût
30 EUR (€)
Mp4
Triangulaire-low.mp4
Matériaux
Contreplaqué 3 mm
PMMA transparent 3 mm
PMMA coloré 3 mm
Billes 5 mm
1 vis et boulon M3 x 20mm
Outils
Découpe laser
Étape 1 - Découpe des pièces
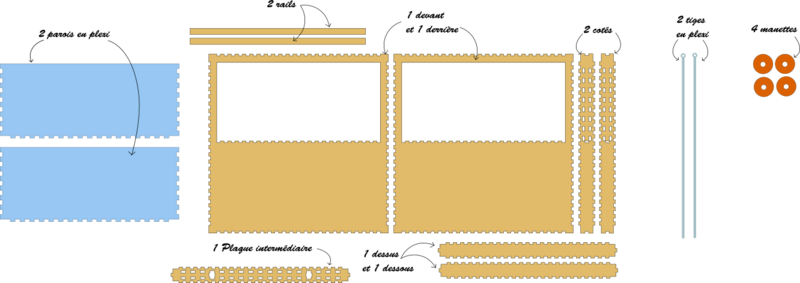
- Découper à la laser les différentes parois de la boite en bois (2 cotés, 1 devant, 1 derrière, 2 rails, 1 plaque intermédiaire)
- Découper à la laser les parois en PMMA ainsi que les tiges
- Découper à la laser les manettes dans des chutes de PMMA coloré
Étape 2 - Assemblage de la boîte
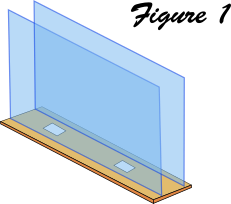
1. Assembler les parois en PMMA sur la plaque intermédiaire en bois (cf figure 1)
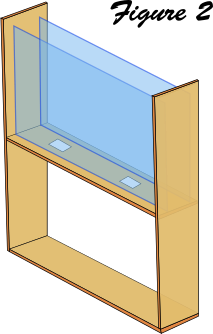
2. Assembler les cotés et le dessous (cf figure 2)
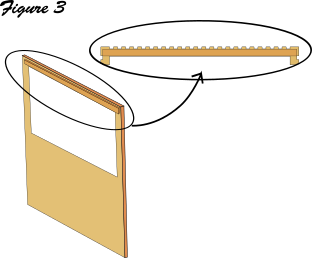
3. Coller les rails à l'intérieur des parois en bois "devant" et "derrière" (en dessous des crans, cf figure 3)
4. Assembler les parois en bois devant et derrière (cf figure 4)
Étape 3 - Ajout des billes
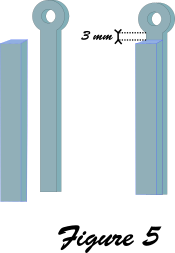
- Coller les tiges en PMMA (cf figure 5)
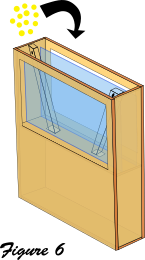
- Insérer les tiges en PMMA, entre les parois en PMMA, les faire passer dans les trous de la plaque intermédiaire.
- Verser les billes entre les tiges (si besoin fabriquez-vous un entonnoir en papier) en les resserrant petit à petit.
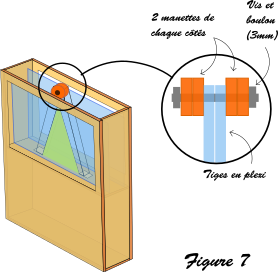
- Rejoindre les extrémités des tiges avec les manettes et une vis de 3mm (cf figure 7)
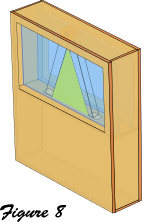
- Refermer la boite
Published



 Français
Français English
English Deutsch
Deutsch Español
Español Italiano
Italiano Português
Português